Statistika i Minitab - Linearna regresija i Metoda najmanjih kvadrata
Statistika i Minitab - praktična primena
Kada koristiti linearnu regresiju?
Šta je regresija u statistici?
Regresija je odnos dve promenjive, od kojih jedna zavisi od druge. Promena nezavisne promenjive X utiče na promenu zavisne promenjive Y.
Šta je linearna regresija?
Linearna regresija je uzročno-posledični odnos dve promenjive- nezavisne X i zavisne Y. Linearnost ukazuje da promena nezavisnog faktora X dovodi do linearnog smanjenja ili povećanja zavisne promenjive Y.
U statistici, linearna regresija se predstavlja jednačinom:
Y=aX+b
Kada koristiti linearnu regresiju?
Matematičkim jezikom odgovor je: kada su zavisna promenjiva (Y) i nezavisne promenjive koje možda utiču na nju (X1,2,…) kontinualne veličine i kada pretpostavljamo da je uticaj linearan.
Nematematički odgovor bi bio: ako pretpostavljamo da:
- rezultat našeg eksperimenta zavisi od određenog broja faktora
- zavisnost je linearna, tj. ako neki faktor raste ili opada, naša merena veličina raste ili opada istom brzinom (ili opada i raste)
- merena veličina i faktori koji utiču na nju se mogu prikazati kao decimalni brojevi (napr. visina, težina, cena,…)
koristeći Minitab program, lako ćemo proveriti našu pretpostavku primenom linearne regresije.
Metoda najmanjih kvadrata u linearnoj regresiji
Vršimo uzorkovanje i prikupili smo podatke. Primetili smo da za svaku vrednost neke promenjive X, ono što smo merili – naše Y, menja vrednost.
Ako je promena vrednosti Y-a slična promeni vrednosti X-a, pretpostavljamo da postoji linijska zavisnost.
U tom slučaju možemo odrediti pravu na grafiku koja prikazuje linearnu zavisnost Y-a od X-a i kažemo da je:
Y= βo + β1*X
U realnom svetu, dobijene vrednosti Y nikada nisu apsolutno identične očekivanim vrednostima (onome što izračunamo kada X-u dodelimo određenu vrednost).
Za svako X, izmereno Y se razlikuje od očekivanog Y. Te razlike su REZIDUALI.
U matematici, a i u praksi, je prihvaćeno da je jedan od najboljih načina za određivanje koeficijenata βo i β1 (koji nam određuju linearnu regresionu pravu) METODA NAJMANJIH KVADRATA.
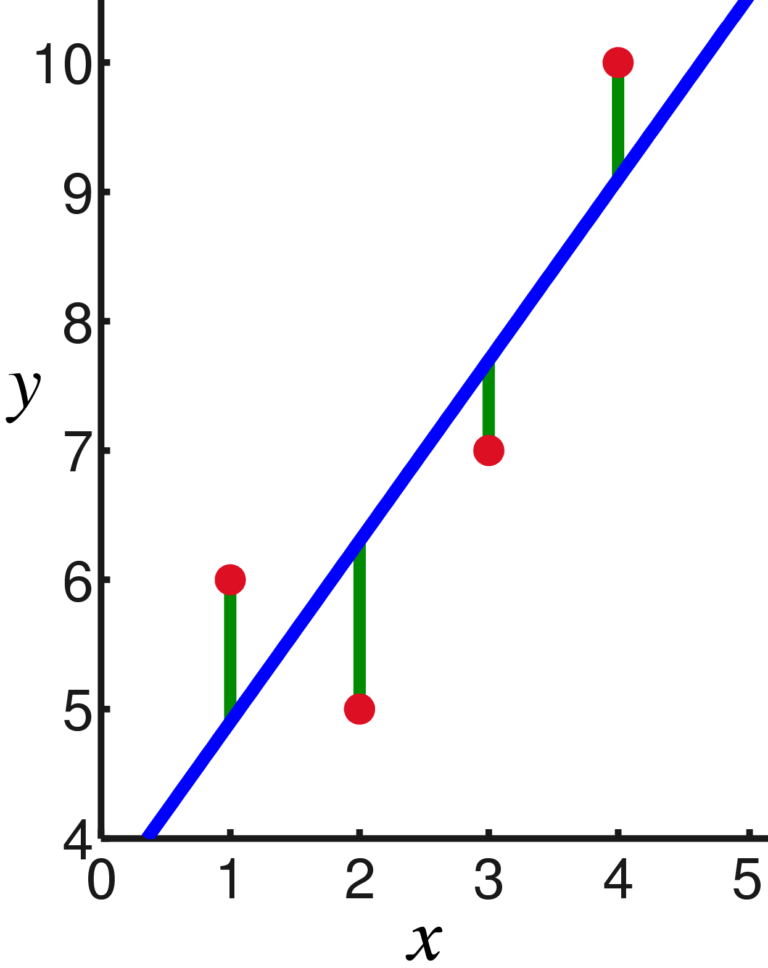
- Plavo je regresiona prava– na njoj se nalaze očekivane vrednosti Y-a za razne vrednosti X-a.
- Crveno su izmerene vrednosti, vrednosti dobijene uzorkovanjem.
- Zeleno su reziduali, razlike izmedju očekivane i dobijene vrednosti.
Za svako izmereno Y, računa se razlika dobijenog i očekivanog Y-a.
Neke razlike su pozitivne, neke su negativne, tj. neke dobijene vrednosti Y-a su veće od očekivanih, a neke su manje. Da se ne bi anulirala (potrla) odstupanja (reziduali), kvadriramo ih.
Najbolju linearnu pravu biramo (računamo) tako da je suma razlika svih odstupanja dobijenih Y-a od očekivanih (izračunatih) minimalna. Optimalna prava, kod koje je razlika kvadrata minimalna se naziva FITOVANA prava.
Zbog toga se ovaj način zove Metoda najmanjih kvadrata.
Minitab sam računa Fitovanu pravu, reziduale i koeficijente βo i β1.
Statistika i Minitab u određivanju i tumačenju KOEFICIJENTA KORELACIJE ρ
Koeficijent korelacije je statistička mera jačine veze izmedju dve promenjive.
Vrednosti se kreću od -1 do 1.
- kada je ρ= 0, ne postoji veza izmedju promenjivih.
- kada je ρ= -1 i kada je ρ= 1, u pitanju je apsolutna povezanost dve promenjive.
- u praksi se najčešće uzima da je jaka korelacija ako je [-1, 0.65] < ρ < [1, 0.65].
VAŽNO: i ako je ρ ≈ 1 ili -1, NE PODRAZUMEVAJTE uzročno- posledičnu vezu. Analizirajte podatke, pa onda donesite zaključak.
Primer jake korelacije bez postojanja uzročnosti:
Nekoliko studija je ukazalo na jaku pozitivnu korelaciju izmedju prodaje sladoleda i broja davljenja u primorskim mestima.
Kako prodaja sladoleda doprinosi slučajevima davljenja?
Baš nikako.
Bez obzira što je korelacioni koeficijent blizu jedinici, uzročnost ne postoji.
Uzročnost postoji izmedju sezone i broja sunčanih dana i prodaje sladoleda, sa jedne strane i broja sunčanih dana i povećanog broja slučajeva davljenja, sa druge strane.
Ako želite više da saznate o ovome, pogledajte video:
Metoda najmanjih kvadrata i objašnjenje NAGIBA I ODSEČKA (koeficijenti βo i β1)
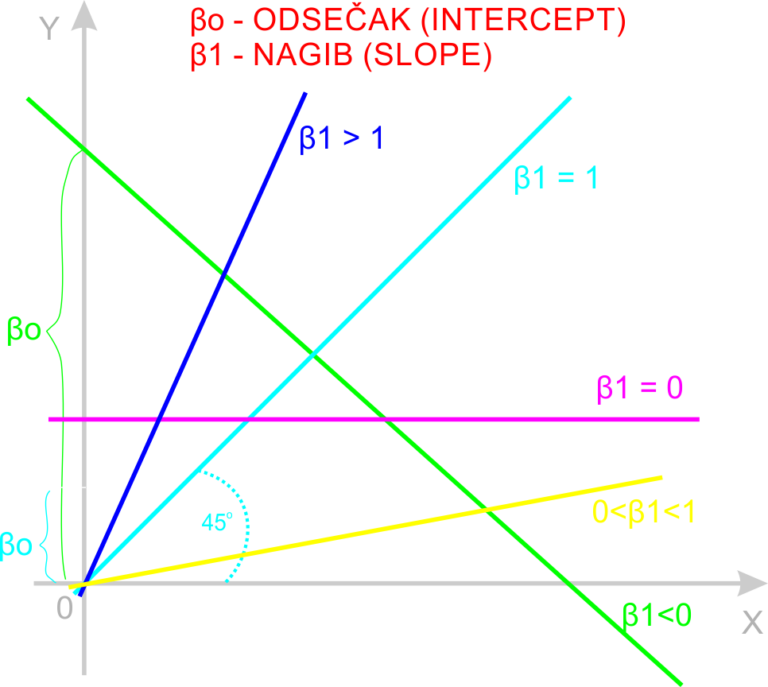
Koeficijent βo određuje ODSEČAK (intercept). To je očekivana vrednost Y-a, kada je X=0.
Koeficijent β1 nam govori kakav je NAGIB prave.
- Ako je β1 > 0, Y raste kada X raste.
- Ako je β1 < 0, Y opada kada X raste.
- Ako je β1 = 0, Y je paralelno sa X-osom. U tom slučaju, za bilo koju vrednost X-a, Y je konstantna veličina i jednaka je βo.
- Ako je β1 = 1, prava je pod uglom od 45o.
- Što je β1 veće od 1, Y brže raste u odnosu na X.
- Što je β1 manje od 1, Y brže opada u zavisnosti od X-a.
ZADATAK 1 - Metoda najmanjih kvadrata i linearna regresija u Minitabu
U tabeli je dat bruto godišnji prihod 10 država (u milijardama dolara) i dužina puteva (u hiljadama kilometara) koji se izgrade tokom godine u svakoj od tih država.
- Odrediti koeficijente βo i β1 tako da prava y=βo + β1*x najbolje odgovara podacima iz tabele u smislu metoda najmanjih kvadrata.
- Kolika je varijansa slučajne greške?
- Koliko je y za x= 50?
- Kolika je fitovana vrednost i rezidual za x=31,33?
- Testirati pouzdanost regresije. Obrazložiti.
- Kolika je standardna greška za nagib (slope) i odsečak (intercept)?
- Odrediti koeficijent korelacije izmedju x i y.
- Testirati hipotezu da je ρ=0.
- Prikazati grafik regresione prave sa granicama intervala poverenja i intervala predikcije.
- Analizirati reziduale.
| BPD | Putevi |
| 12.86 | 61.40 |
| 7.14 | 41.34 |
| 17.14 | 79.21 |
| 31.33 | 130.04 |
| 21.43 | 93.55 |
| 51.43 | 212.86 |
| 25.71 | 110.42 |
| 34.29 | 146.89 |
| 27.14 | 116.89 |
| 57.14 | 236.04 |
ZADATAK 2 - Metoda najmanjih kvadrata i linearna regresija u Minitab programu
U tabeli je dat iznos investicija jedne firme tokom 14 godina i iznosi profita kao rezultat investiranja (u milionima dinara).
| Investirano | Profit |
| 51.44 | 11.77 |
| 28.56 | 9.91 |
| 68.56 | 11.32 |
| 125.32 | 12.58 |
| 85.72 | 13.36 |
| 205.72 | 26.41 |
| 102.84 | 15.77 |
| 137.16 | 18.98 |
| 108.56 | 19.7 |
| 228.56 | 28.72 |
| 63.27 | 13.95 |
| 51.44 | 10.03 |
| 191.61 | 25.77 |
| 36.15 | 14.12 |
- Odrediti koeficijente βo i β1 tako da prava y=βo + β1*x najbolje odgovara podacima iz tabele u smislu metoda najmanjih kvadrata.
- Kolika je varijansa slučajne greške?
- Koliki je fitovani profit ako se investira 20 miliona, a koliki je ako se investira 300 miliona?
- Kolika je fitovana vrednost i rezidual za x=51,44?
- Testirati pouzdanost regresije. Obrazložiti.
- Koliko je model dobar?
- Kolika je standardna greška za nagib (slope) i odsečak (intercept)?
- Odrediti koeficijent korelacije izmedju x i y.
- Testirati hipotezu da je ρ=0. Obrazložiti izračunati koeficijent.
- Prikazati grafik regresione prave sa granicama intervala poverenja i intervala predikcije.
- Analizirati reziduale. Postaviti hipoteze i izvući zaključke.
Zakažite termine online časova.
Raspoloživi termini:
Bilo koji dan u nedelji
10-12h
14-16h
Cena online časova Minitab i statistika:
2400 din/ 1h
Časove možemo snimiti tako da Vam ostaju zauvek!