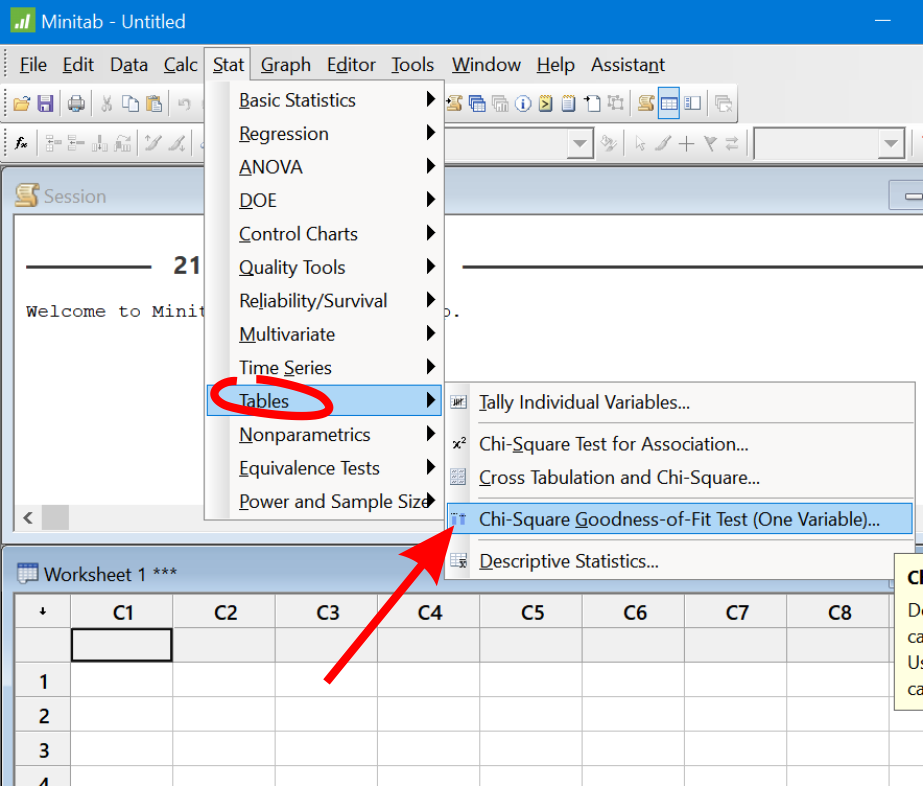
Program za statistiku Minitab i Hi kvadrat test
Hi kvadrat test se najčešće koristi za ispitivanje da li:
- podaci uzorkovanja dolaze iz populacije sa normalnom raspodelom (U Minitabu: Goodness of Fit Test– zadatak 1, 2, 3);
- dve kategorijske promenjive imaju vezu ili su nezavisne- rezultat testa je binaran, „da“ ili „ne“ (Contingency Table Test, u Minitabu: Chi Square Test for Association – zadatak 4 i 5);
- postoji razlika izmedju očekivanih i dobijenih rezultata merenja, pri testiranju kategorijske promenjive.
Program za statistiku Minitab i primena Hi kvadrat testa
Ako želite više da saznate i naučite o Hi-kvadrat raspodeli i primeni, na ovom linku imate nekoliko edukativnih videa:
Uslovi da se sprovede Hi-kvadrat test za proveru normalnosti
χ² test za proveru normalnosti može da se koristi ako su podaci:
- dobijeni slučajnim uzorkovanjem,
- kategorijske promenjive.
Ako su podaci kontinualni, pre sprovođenja testa potrebno je grupisati ih u raspone od-do i za tako definisane raspone odrediti frekvencije.
Program za statistiku Minitab i Hi-kvadrat Goodness of Fit Test
Eng: Chi Square Goodness of Fit Test
χ² test za proveru normalnosti, u Minitabu Goodness of Fit Test nam govori da li podaci dobijeni uzorkovanjem dolaze iz populacije sa Normalnom raspodelom koja ima određenu srednju vrednost i standardnu devijaciju N(µ, δ).
Poređenjem dobijenih vrednosti i očekivanih vrednosti se donosi zaključak.
Hipoteze kod χ² testa su:
Ho: podaci dobijeni uzorkovanjem imaju normalnu raspodelu sa datim parametrima.
Ha: podaci nemaju normalnu raspodelu.
OČEKIVANA VEROVATNOĆA I OČEKIVANA VREDNOST
Pre nego što pređemo na zadatke, objasnićemo kako se u Excelu može izračunati očekivana verovatnoća i OČEKIVANE VREDNOSTI. Biće nam potrebno za rešavanje zadataka za proveru normalnosti pomoću χ² testa.
Ako pretpostavimo da uzorak eksperimenta dolazi iz populacije sa Normalnom raspodelom N (µ, δ), verovatnoća da je x < b (u zadatku 1, b=1, 2, …8, 9, >9) se u Excelu dobija formulom =NORMDIST(b,µ,δ,TRUE).
Očekivana verovatnoća da je x u intervalu (a, b] je =NORMDIST(b,µ,δ,TRUE)-NORMDIST(a,µ,δ,TRUE).
Očekivana vrednost se dobija množenjem očekivane verovatnoće i ukupnog broja uzoraka.
ZADATAK 1 Hi-kvadrat Goodness of Fit Test
Ispituje se efekat dijete na 150 ljudi sa prekomernom težinom. U tabeli je dato koliko ljudi je izgubilo 1, 2, …9 i više od 9 kilograma posle 30 dana.
χ² testom proveriti da li dobijeni podaci odgovaraju normalnoj raspodeli N(5, 2,5).
ZADATAK 2 Hi-kvadrat Goodness of Fit Test
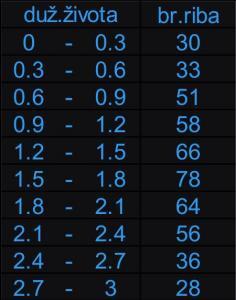
Ispituje se dužina života u godinama jedne vrste riba u uzorku veličine 500. U tabeli su dati podaci u rasponima od-do:
χ² testom proveriti da li dobijeni podaci odgovaraju normalnoj raspodeli:
- N (1.6 ; 0.9)
- N (1.4 ; 0.8)
Obrazložiti rezultate.
ZADATAK 3 Hi-kvadrat Goodness of Fit Test
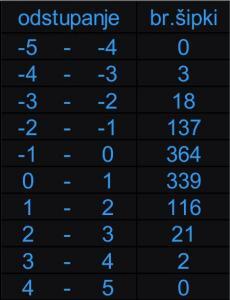
Ispituje se odstupanje u milimetrima u proizvodnji šipki od postavljenog standarda. Uzorkom je obuhvaćeno 1000 šipki.
U tabeli su dati podaci odstupanja u milimetrima u rasponima od-do:
χ² testom proveriti da li dobijeni podaci odgovaraju standardnoj normalnoj raspodeli.
Tabele kontigencije i Chi Square Test for Association
Tabele kontigencije u statistici se koriste da se prikažu frekvencije 2 kategoričke promenjive sa ciljem da se utvrdi da li su te dve promenjive zavisne.
Ako se povezanost proverava χ² testom, rezultat je da / ne.
Hipoteze su:
Ho: dve promenjive nisu povezane, nezavisne su jedna od druge.
Ha: postoji zavisnost izmedju dve promenjive.
ZADATAK 4 – Hi-kvadrat test – Tabele kontigencije (provera zavisnosti)
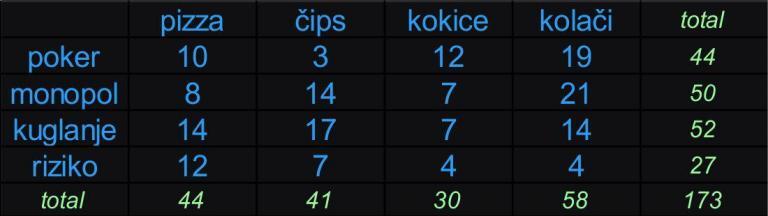
U jednoj igraonici se ispituje koju hranu kupuju igrači koji igraju različite igre, sa ciljem da se utvrdi postoji li povezanost igre koja se igra sa vrstom izabrane hrane. Rezultati su dati u tabeli kontigencije.
Da li se može zaključiti da ljudi koji biraju određenu igru preferiraju i određenu hranu tokom igranja?
Zadatak 5, Hi-kvadrat test – Tabele kontigencije
Trgovinski lanac ispituje da li postoji povezanost prodaje određene grupe artikala i lokacije prodavnice.
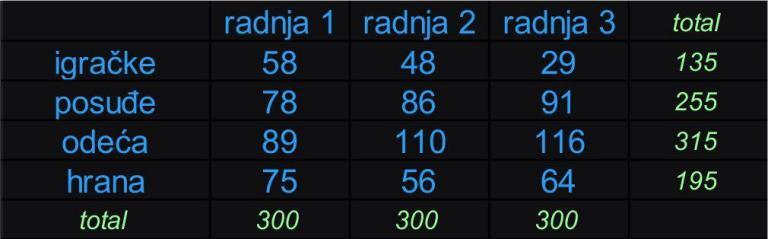
- Prvi način merenja koji su izvršili je obuhvatio za svaku lokaciju po 300 prodatih komada bilo čega i onda su prebrojali koliko kojih vrsta artikala je prodato u okviru tih 300 komada. Podaci su u tabeli 1.
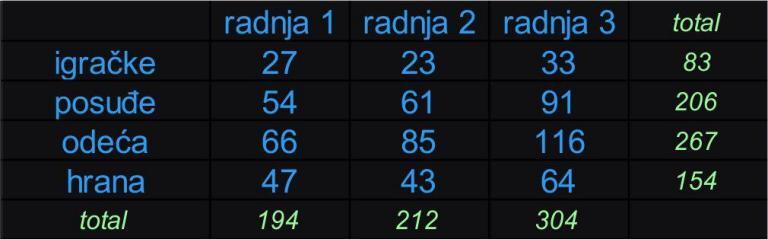
Drugi način merenja je obuhvatio prodaju na kraju radne nedelje za svaku prodavnicu posebno i u okviru nedeljne prodaje je prebrojano koliko artikala po grupama je prodato.
Podaci su dati u tabeli 2.
TABELA 1
TABELA 2
Da li postoji zavisnost prodaje određene vrste proizvoda u odnosu na lokaciju prodavnice mereno na jedan i drugi način?
Pročitajte detaljnije o primenama Minitaba u svetu biznisa, agendi našeg kursa i časovima za pripremu ispita na linku: Minitab statistički softver za biznis.
Potrebna Vam je pomoć za pripremu ispita iz Statistike i Minitaba?
Želite li da sa Vama proradimo zadatak, projekat, analizu podataka?
Zakažite termine online časova.
Raspoloživi termini:
Bilo koji dan u nedelji
10-12h
14-16h
Cena online časova Minitab i statistika:
2400 din/ 1h
Časove možemo snimiti tako da Vam ostaju zauvek!